What Is The Period Of The Cosecant Function Graphed Below
Okay, confession time. When someone mentions the word "period" in math, my brain immediately conjures up images of high school algebra class. You know, the stuff that felt like deciphering ancient hieroglyphics while simultaneously trying to remember if I had homework? Yeah, that kind of period. And then, as if that wasn't enough, they throw in these fancy functions with names that sound like obscure Latin phrases. Today, we're going to chat about one such character: the cosecant function.
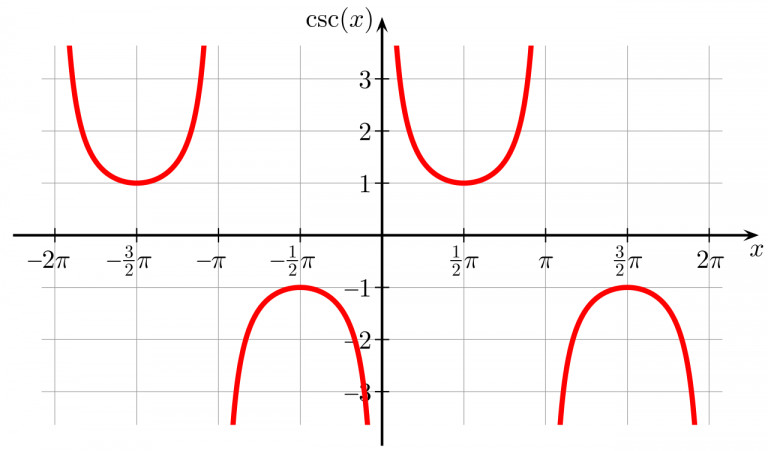
Now, I'm not saying math is inherently boring. It’s just that sometimes, it feels like it’s speaking a different language. And that’s where this little graph comes in. We’re looking at a picture. A picture of the cosecant function. And the question is: what’s its period?
Let's be real. The word "period" in math can be a little… confusing. It’s not like your menstrual cycle (though that has its own fascinating rhythm). In math, it's more about repetition. Like a catchy song that loops back to the beginning. A musical riff that just keeps on giving. The cosecant function, bless its mathematical heart, also loves a good repeat. It’s got a pattern, and this pattern keeps showing up. Over and over.
So, what exactly are we looking for on this graph? We’re trying to find the length of one full cycle. Imagine you’re following a little ant crawling along the cosecant curve. You want to know how long it takes for that ant to go through one complete journey and end up exactly where it started, facing the same direction, ready to do it all again. That journey’s length? That’s the period.
It's like finding that perfect moment in a song where the beat drops, and you know the chorus is about to hit. That’s a period! Or maybe the time it takes for your favorite TV show to air a whole season. You watch it, you’re hooked, and then you’re eagerly waiting for the next season to start. That’s a period of enjoyment, for sure.
Now, this cosecant function is a bit of a drama queen. It doesn't have a smooth, continuous line like some of its more well-behaved friends (looking at you, sine and cosine). Oh no. The cosecant likes to show off with its dramatic dips and soaring peaks. It has these things called asymptotes, which are basically lines it gets super, super close to, but never actually touches. Like a celebrity trying to avoid the paparazzi. It's a whole spectacle!
These asymptotes are important clues, though. They help us pinpoint where one cycle ends and the next begins. Think of them as the invisible fences marking the boundaries of each repeating segment of the graph. They show us where the function throws its hands up and says, "Nope, can't go there!"
So, when we look at the graph, we’re scanning from left to right. We find a point, and then we keep going until we see that exact same pattern repeat. It might be a peak followed by a dip, or a dip followed by a peak. The key is that it’s exactly the same configuration. No funny business. No unexpected plot twists.
The thing about the cosecant function, and its trusty sidekick the secant function (they're basically cousins, but with a slight attitude difference), is that their fundamental period is tied to something very familiar. Something you probably learned about in your early math days, perhaps even before you knew what a function was. It’s a number that defines a full circle. A full rotation.
If you’ve ever drawn a circle or talked about angles in degrees, this number should ring a bell. It’s the number that gets you all the way around. The number that brings you back to the start. It’s a constant, a champion of repetition.
Let’s just say, if the sine and cosine functions have a period of, you know, that whole circle thing, the cosecant follows suit. It inherits that same cyclical DNA. It’s like saying, if your sibling’s favorite color is blue, there’s a pretty good chance you’ve got a soft spot for blue too, especially when you’re closely related.
So, when you gaze upon the glorious, wavy, and sometimes a little bit wild graph of the cosecant function, and someone asks you about its period, take a deep breath. Remember the song that loops. Remember the ant’s journey. And most importantly, remember that fundamental number that completes a full circle. That, my friends, is your answer.

It’s a number that’s as constant as the tides, as reliable as the sunrise, and as fundamental to a full cycle as a donut hole is to a donut (a somewhat lopsided donut, perhaps, but a donut nonetheless). The period of the cosecant function? It’s that magical measurement that tells us when the party starts all over again. And trust me, this function loves a good party.
