What Is The Lcm Of 42 And 28

Ever found yourself staring at a math problem and thinking, "Why would I ever need this in real life?" Well, today we're going to dive into something that sounds a little technical but is actually quite handy and surprisingly fun: finding the Least Common Multiple (LCM) of numbers, specifically 42 and 28.
You might be wondering, "What's the big deal with the LCM?" Think of it like this: the LCM is the smallest number that two or more numbers can both divide into perfectly. It’s like finding the smallest common meeting point for different cycles or schedules. For beginners, it’s a fantastic way to start building a foundational understanding of number relationships. For families, it can be a neat little puzzle to tackle together, turning math practice into a game. Hobbyists, especially those who dabble in things like knitting patterns, music timing, or even planning shared events, might find the LCM incredibly useful for coordinating different frequencies or cycles.
Let’s break down the LCM of 42 and 28. Imagine you have two friends, Alex and Ben. Alex visits the park every 42 days, and Ben visits every 28 days. When will they next see each other at the park on the same day? That's where the LCM comes in! It will tell you the minimum number of days before their schedules align again. It’s a practical way to predict shared occurrences.

There are a few ways to find the LCM. One simple method is to list out the multiples of each number until you find the first one they have in common. For 42, the multiples are: 42, 84, 126, 168, ... For 28, the multiples are: 28, 56, 84, 112, ... See that? The first number that appears in both lists is 84. So, the LCM of 42 and 28 is 84. They will next meet at the park in 84 days!
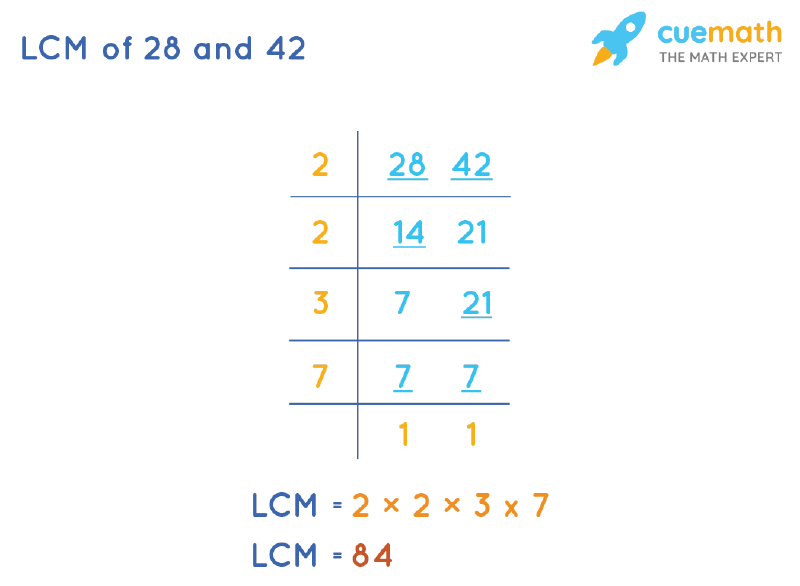
Another popular method, especially for larger numbers, is using prime factorization. You break down each number into its prime building blocks. 42 = 2 x 3 x 7 28 = 2 x 2 x 7 (or 2² x 7) To find the LCM, you take the highest power of each prime factor that appears in either factorization. In this case, we have 2² (from 28), 3 (from 42), and 7 (from both). So, LCM = 2² x 3 x 7 = 4 x 3 x 7 = 84. It's like gathering all the necessary ingredients to build the smallest common structure.
A simple tip for getting started is to practice with smaller numbers first. Try finding the LCM of 4 and 6, or 10 and 15. You'll quickly get the hang of listing multiples or using prime factors. Don't be afraid to grab a piece of paper and doodle it out; visual aids can be incredibly helpful.
Finding the LCM might seem like just another math exercise, but it’s a versatile tool that can simplify planning and understanding recurring events. It’s a little bit of number magic that makes everyday life a bit more predictable and organized.
