What Is 3 6 In Simplest Form

Hey there, math explorers! Ever find yourself staring at numbers like 3/6 and wondering, "What in the world does that even mean in its simplest form?" Don't worry, you're not alone! Sometimes math can feel like trying to untangle a really stubborn headphone cord, right? But trust me, simplifying fractions is way less frustrating than that. Think of it as giving your fraction a nice, tidy little haircut. We're going to chop off any unnecessary bits until it's as lean and mean as can be.
So, let's dive right in. We're talking about the fraction 3/6. See those numbers? The top one is the numerator, and the bottom one is the denominator. The numerator tells us how many parts we have, and the denominator tells us how many total parts make up the whole. Easy peasy, right? It's like having a pizza cut into 6 slices, and you've got 3 of them. Yum!
Now, the quest for the "simplest form" is all about finding the smallest possible numbers that still represent the same amount. It's like finding the shortest path between two points – we want the most efficient way to say it. And for 3/6, there's definitely a shorter, sweeter way to express it.
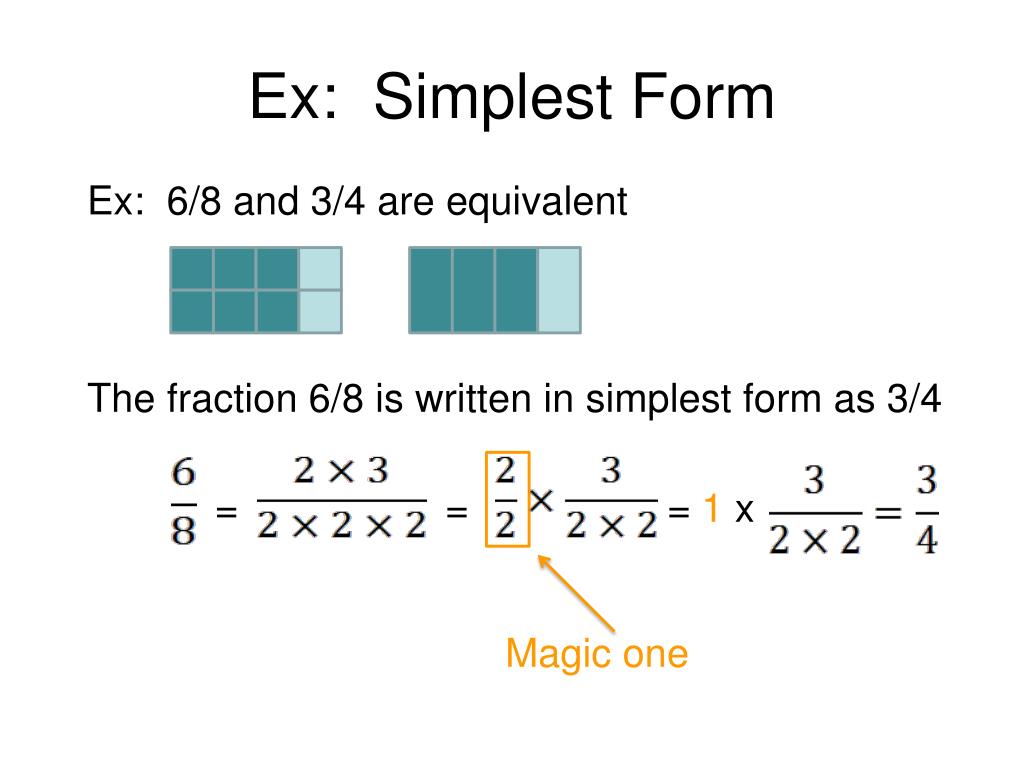
How do we do it? Well, the secret sauce is finding a common factor. A common factor is a number that can divide both the numerator and the denominator without leaving any leftovers. Think of it as a superhero number that can conquer both parts of the fraction. And for 3 and 6, we've got a pretty obvious superhero ready to swoop in.
Let's look at our superhero candidates. Can we divide 3 by 1? Yep. Can we divide 6 by 1? Yep. So, 1 is a common factor. But is it the biggest common factor? Probably not. We want to be more efficient, remember? Like finding a shortcut on your commute!
Okay, what about the number 2? Can we divide 3 by 2 without a remainder? Nope. 3 is an oddball when it comes to 2. So, 2 isn't our superhero for both numbers. Bummer.
How about the number 3? Can we divide 3 by 3? You betcha! That gives us a nice, round 1. Now, can we divide 6 by 3? Absolutely! 6 divided by 3 is 2. Aha! We found our superhero!
So, our common factor, and in this case, our greatest common factor (GCF), is 3. This is the magic number that's going to help us simplify our fraction. The GCF is like the ultimate VIP pass – it’s the largest number that goes into both!
Here's the fun part. We take our original fraction, 3/6, and we're going to divide both the numerator and the denominator by our superhero, 3. It's like giving them both a dose of super-strength!
So, for the numerator: 3 ÷ 3 = 1. See? It’s like the 3 decided to become a proud little 1. And for the denominator: 6 ÷ 3 = 2. The 6 bravely transformed into a sleek 2. Ta-da!
And what do we have now? We have the fraction 1/2! 🎉
So, in its simplest form, 3/6 is equal to 1/2. Mind. Blown. Right?
Think about our pizza again. If you have 3 slices out of 6, you have exactly half of the pizza. If you ate 3 slices, and there were 6 total, you've definitely enjoyed half of that deliciousness. So, whether you say you ate 3/6 of the pizza or 1/2 of the pizza, you're saying the same thing! It's just that 1/2 sounds a lot more… concise. And who doesn't love conciseness? It's like getting to the punchline of a joke faster.
Let's quickly recap the strategy. It's pretty straightforward:
Step 1: Find the Greatest Common Factor (GCF)
Look at your numerator and your denominator. What's the biggest number that divides evenly into both of them? If you're not sure, you can always list out the factors of each number.
For 3, the factors are: 1, 3.
For 6, the factors are: 1, 2, 3, 6.
See? The largest number that appears in both lists is 3. So, our GCF is 3.
Step 2: Divide Both Numbers by the GCF
Take your numerator and divide it by the GCF. Take your denominator and divide it by the GCF. This is where the magic happens!
Numerator: 3 ÷ 3 = 1
Denominator: 6 ÷ 3 = 2
Step 3: Write Your New, Simplified Fraction
Put your new numerator over your new denominator. And you've got it!
1/2
And that, my friends, is 3/6 in its simplest form. It's like a transformation sequence from a slightly clunky number to a sleek, streamlined one.
Why is this important, you ask? Well, simplifying fractions makes them much easier to understand and work with. Imagine trying to add 3/6 + 2/6. It's doable, but what if you had to add 3/6 + 1/12? Suddenly, it gets a bit more complicated. But if you simplify 3/6 to 1/2 first, then the problem becomes 1/2 + 1/12, which is a lot less intimidating. See? It's like clearing the clutter from your desk so you can actually get your work done!
Also, when you're comparing fractions, it's way easier if they're in their simplest forms. Comparing 3/6 and 4/8 feels like a guessing game. But simplify them? 3/6 becomes 1/2, and 4/8 also becomes 1/2! Boom! You immediately know they're the same. It's like having a secret code that makes everything clearer.
Sometimes, you might have a fraction where the only common factor is 1. For example, what's 2/5 in its simplest form? Let's think. Factors of 2 are 1, 2. Factors of 5 are 1, 5. The only common factor is 1. So, 2/5 is already in its simplest form. It's like a perfectly formed snowflake – no need to change a thing!
Or consider 7/14. What's the GCF of 7 and 14? Well, 7 goes into 7 (once), and 7 goes into 14 (twice). So, the GCF is 7. Divide both by 7: 7 ÷ 7 = 1, and 14 ÷ 7 = 2. So, 7/14 simplifies to 1/2. Another half! The universe loves halves, apparently.
Don't be afraid to experiment! Grab a piece of paper, pick a fraction, and try to find that GCF. It might take a little practice, but soon you'll be a fraction-simplifying ninja. You'll be spotting those common factors like a hawk spotting its lunch. It's a superpower, really!
Remember, every fraction has a simplest form. It's just waiting to be discovered. And the process of finding it is a wonderful way to understand how numbers relate to each other. It's like learning a new language, a language of proportions and equality.

So next time you see a fraction that looks a bit… wordy, just remember our pizza analogy, our superhero factors, and the simple steps to simplify. You've got this! You can conquer any fraction, big or small. And with each simplification, you're not just making math easier, you're making it a little bit more beautiful, a little bit more elegant. Go forth and simplify, you brilliant mathematical wizards!
