The Slope Of A Horizontal Line Will Always Be

Alright, so picture this: you're at a café, right? Sipping on your lukewarm latte, trying to look sophisticated. And then, BAM! Someone asks you about the slope of a horizontal line. You probably think, "Is this a trick question? Did I accidentally order the 'existential dread' special?" But fear not, my caffeinated comrades, because the answer is actually as flat and uneventful as your grandma's pancake batter. And trust me, we're going to dive into this with all the excitement of a snail race, but way more fun.
So, what exactly is this elusive slope we're talking about? Think of slope as the "steepness" of a line. If you're hiking, a steep slope means you're going to be huffing and puffing like a Victorian gentleman climbing a single flight of stairs. A gentle slope is more like strolling through a park, perhaps with a poodle named Pierre. And a horizontal line? Well, that's the line that's so flat, it makes a freshly ironed shirt look like a crumpled napkin.
Imagine you're drawing a line on a piece of graph paper. A horizontal line is like drawing it from left to right, perfectly level. No hills, no valleys, not even a tiny speed bump. It just… goes. It's the line that's completely content with its lot in life, not aspiring to be anything more than… well, horizontal.

Now, let's get a little mathy, but in a chill, "I'm not taking a pop quiz" kind of way. Slope is often represented by the letter 'm'. Fancy, right? And how do we calculate this mysterious 'm'? It's usually the "rise over run." The "rise" is how much the line goes up or down (the change in the y-values), and the "run" is how much it goes across (the change in the x-values). Think of it as your vertical progress divided by your horizontal progress. Easy peasy, lemon squeezy.
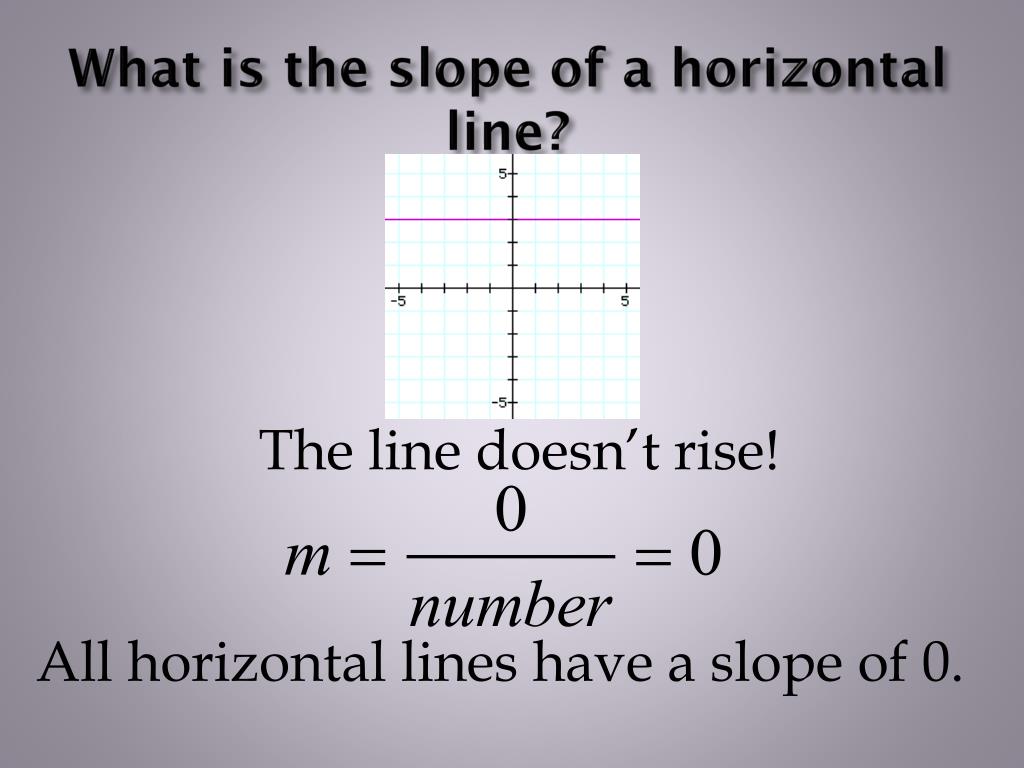
So, for our horizontal hero, what's the rise? If the line is truly horizontal, it doesn't go up or down at all. It's like a meerkat standing perfectly still – no vertical movement whatsoever. So, the "rise" is a big fat zero. Zilch. Nada. The "rise" is zero.
And what about the "run"? Well, the line is definitely moving across, right? It's traveling from the left side of the paper to the right. So, there is a run. Let's say it runs 5 units. The run could be 1 unit, 100 units, or even the entire width of the universe, and it wouldn't change the fundamental fact about the rise.
So, we have our slope 'm' looking like this: 0 (the rise) divided by… well, any number greater than zero (the run). What happens when you divide zero by any number that isn't zero? Take a moment. Contemplate the universe. Think about sharing a pizza with friends – if you have zero pizzas to share amongst your friends, everyone gets… nothing. The result is still nothing.
Therefore, 0 divided by any number (other than zero) is always zero. And that, my friends, is why the slope of a horizontal line will always be zero.
It's like this: Imagine you're trying to convince a particularly stubborn mule to move. If the mule is already standing perfectly still, you can push and shove all you want (that's your "run"), but it's not going to budge upwards (that's your "rise"). The mule's vertical progress is zero. Hence, the effectiveness of your pushing (the slope) is zero. The mule remains unmoved, much like a horizontal line on a graph.
Let's take it a step further. What if you tried to calculate the slope of a vertical line? Now, that's a whole other ballgame. A vertical line goes straight up and down. It has a massive "rise" (it shoots up like a rocket!), but its "run" is zero. It doesn't move sideways at all. So, you'd be trying to divide a number by zero. And as anyone who has ever tried to divide by zero (which, to be fair, is most people by accident) knows, that's a big mathematical no-no. It's like trying to un-ring a bell. It's undefined. It breaks the internet. It causes existential crises in calculators. It's the mathematical equivalent of stepping on a Lego brick in the dark.
But our horizontal line? It's the chill, laid-back cousin of the vertical line. It's not trying to cause a stir. It's just existing, flatly and serenely. Its slope is zero because there's no inclination to change its vertical position. It's perfectly happy staying put, horizontally speaking.
Think about it in real life. A perfectly flat road has a slope of zero. You're not going uphill, you're not going downhill. You're just cruising. A table top? Slope is zero. A still lake? Slope is zero. The line you draw when you're desperately trying to keep your handwriting straight on ruled paper (and failing miserably)? That one might have a slope, but the ideal horizontal line has none.
So, next time someone throws the "slope of a horizontal line" question at you, you can confidently, and perhaps with a slight air of superiority, declare: "It's zero!" You can then add, with a wink, "Because it's not going anywhere interesting, vertically speaking." And if they look confused, just remind them that some things in life are meant to be straightforward, like a good cup of coffee or a perfectly flat line. And sometimes, zero is the most interesting number of all, especially when it signifies perfect, unadulterated flatness.
It's a beautiful concept, really. In a world that's constantly changing, going up and down, and generally being a bit chaotic, there's something wonderfully reassuring about a line that just… stays. It's the Zen master of lines, the stoic philosopher of the coordinate plane. Its slope is zero, and it wears that fact with quiet dignity. So, raise your lukewarm lattes to the humble, the reliable, the undeniably zero-sloped horizontal line!
