On What Does The Angular Momentum Of An Object Depend

Ever watched a figure skater do a dizzying spin? Or maybe you’ve noticed how a spinning top slows down eventually, but it seems to have a mind of its own while it’s going fast? Well, there’s a pretty cool physics concept at play there, and it’s called angular momentum. Now, before you start picturing complicated equations or boring lectures, let me tell you, it's actually a super intuitive idea that pops up in our everyday lives more than you might think. It’s basically the "oomph" something has when it’s spinning.
So, on what does this magical "oomph" depend? Think of it like this: if you're trying to get something to spin, or if something is already spinning, what would make it more spinny, or harder to stop spinning? There are two main ingredients to this spinning pie, and they’re both pretty straightforward.
Ingredient 1: How Much Stuff Is Spinning?
The first thing that influences angular momentum is simply how much mass is involved in the spin. Imagine you’re trying to spin a little toy car versus trying to spin a giant tractor. Which one feels like it has more "oomph" once it’s moving? Yep, the tractor, right?
It’s the same principle. If you have more "stuff" (mass) that’s moving in a circle, it’s going to have more angular momentum. Think about a merry-go-round. If only a couple of kids are on it, it’s pretty easy for an adult to give it a good shove and get it going. But if that merry-go-round is packed with twenty people, it takes a lot more effort to get it spinning, and once it’s going, it’s going to keep going with a lot more power. That extra "oomph" comes from all that extra mass moving around.
We can also think about how that mass is distributed. Imagine you have a really long, thin stick. If you spin it around its center, it has a certain amount of angular momentum. Now, imagine you take that same stick and you tie heavy weights to both ends. If you spin that around its center, it feels like it has way more "oomph," doesn't it? This leads us to our second ingredient.
Ingredient 2: How Far Away Is The Stuff From The Spinny Bit?
This is where things get really interesting and where our figure skater comes in. The second key factor in angular momentum is how the mass is distributed relative to the axis of rotation – basically, how far away the "stuff" is from the center of the spin.
Let’s go back to our figure skater. When they start their spin with their arms and legs extended, they’re spreading their mass out. This makes them spin slower, almost like a majestic, slow-motion pirouette. But then, they pull their arms and legs in close to their body. What happens? Whoosh! They start spinning much, much faster!
Why? Because by pulling their mass closer to their body (the axis of rotation), they’re making it easier for them to spin faster. It’s like they’re saying, "Okay, gravity, you can have this part, but the rest of me is going to really get into this spin!" This principle is incredibly important in physics and explains a lot of neat tricks. The closer the mass is to the center, the faster something can spin for the same amount of "spinning power."
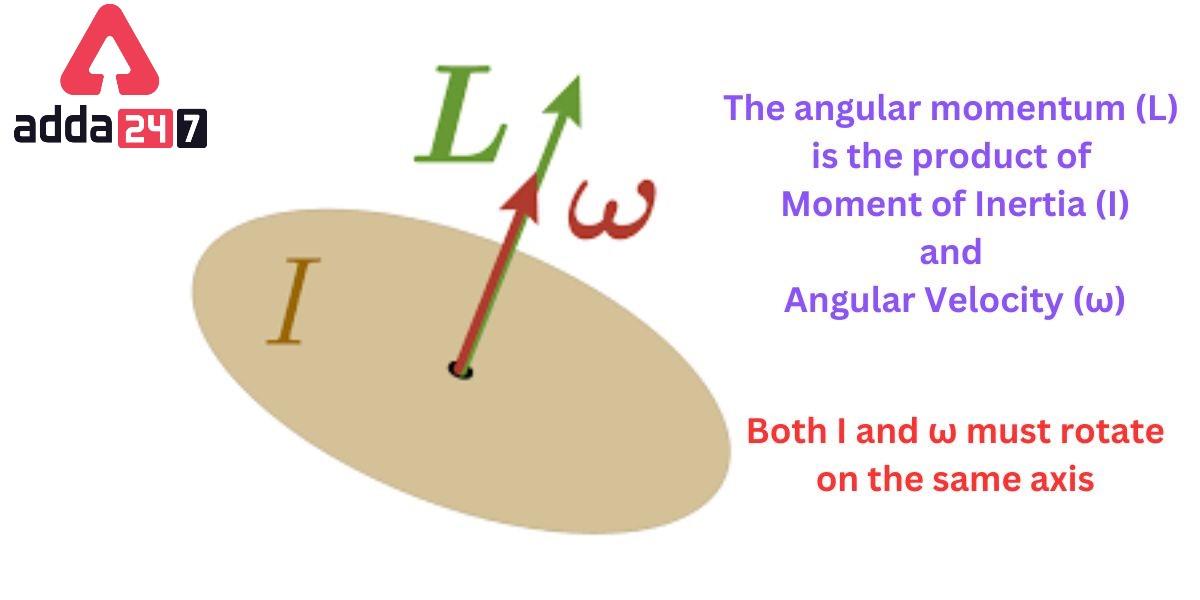
Think about a dancer. When they want to do a fast spin, they tuck their arms in. When they want to slow down and pose, they might extend them out. It's all about managing their moment of inertia, which is the fancy physics term for how resistant an object is to changes in its rotation. And that moment of inertia depends on both the mass and how it’s spread out.
Why Should We Even Care About This "Spinny Oomph"?
You might be thinking, "Okay, that's neat for skaters and tops, but how does this affect my morning commute or my grocery shopping?" Well, the principles of angular momentum are quietly working behind the scenes in so many things we rely on, often in ways that make our lives easier or more interesting.
Take a spinning bike wheel. Its angular momentum helps keep the bike stable. That’s why a bike is much easier to balance when it’s moving than when it’s stopped. The spinning wheel has a sort of "gyroscopic effect" that resists tilting. It’s like the wheel is saying, "Whoa there, partner, let’s keep things upright!"
Or consider the Earth itself. It’s spinning, and it has a massive amount of angular momentum. This is a huge reason why our planet keeps spinning consistently, giving us our days and nights. Imagine if Earth just suddenly decided to stop spinning – that would be a cosmic oopsie of epic proportions! The conservation of angular momentum means that unless something truly enormous acts on it, that spin is going to stay pretty much the same.
Even something as simple as stirring your coffee can illustrate the point. When you stir, you’re imparting angular momentum to the liquid. The faster you stir, and the more vigorously you move the spoon in a circle, the more "spinny oomph" you give the coffee. And you can see how the liquid starts to swirl and move together.
Think about a blender. The fast-spinning blades have a lot of angular momentum, and that's what helps them chop and mix your ingredients. If the motor was weak, or the blades were designed poorly (say, all clumped together), they wouldn't be able to generate enough spinning power to get the job done efficiently.
It’s All About Balance and Motion
So, at its heart, angular momentum is about how much "spinning inertia" an object has. It depends on how much stuff there is (mass) and how that stuff is arranged (distribution of mass). The more mass, and the further that mass is from the center of rotation, the greater the angular momentum, and generally, the harder it is to start or stop the spin.
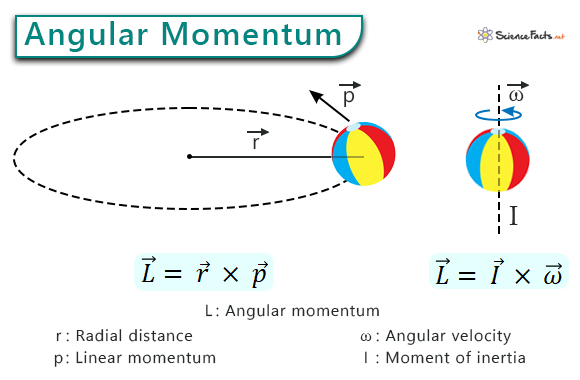
It’s this interplay of mass and its distribution that makes the world go ‘round, quite literally! From the smallest atoms to the largest galaxies, angular momentum plays a fundamental role. It’s the reason why a dancer can spin faster by tucking in their arms, why a bicycle stays upright, and why the universe has such grand, consistent movements. It’s a bit like the universe’s favorite way of saying, "Once you get going, it’s hard to stop this fun!" And that, my friends, is a pretty awesome thought to spin around in your head.
