Lowest Common Multiple Of 15 And 24

Hey there, ever found yourself staring at a math problem and thinking, "Why on earth do I need to know this?" I totally get it! Life throws enough at us – remembering birthdays, finding matching socks, figuring out when the next bus is coming. Do we really need to worry about something called the "Lowest Common Multiple"? Well, stick with me for a few minutes, and I promise to make it surprisingly painless, maybe even a little bit fun. And who knows, you might even find a tiny, quirky reason to care about the Lowest Common Multiple of 15 and 24.
Let's imagine a scenario. Picture two friends, Brenda and Gary. Brenda is super organized and loves to bake. She bakes cookies every 15 days because, well, that's how often she restocks her special chocolate chips. Gary, on the other hand, is a bit more laid-back. He loves to play video games, and he dedicates a gaming session every 24 days to conquer a new level in his favorite epic quest. Now, these two are best buds, and they love to surprise each other with their respective passions. Brenda wants to bake Gary some cookies on a day when he's also finished his gaming marathon. So, the big question is: When will their schedules line up for the first time ever? This, my friends, is where our friendly neighborhood Lowest Common Multiple swoops in to save the day!
Unpacking the "Lowest Common Multiple"
So, what exactly is this Lowest Common Multiple (LCM) thing? Think of it as finding the smallest number that both numbers can happily divide into. It's like finding the shortest time when two recurring events will happen on the same day. They both have their own rhythm, their own beat, and the LCM is the first point where those beats perfectly sync up.
Let's break down the numbers themselves: 15 and 24. They sound pretty ordinary, right? But they have their own little worlds of multiples.
The Multiples of 15: Brenda's Cookie Calendar
Brenda bakes every 15 days. So, her baking days look like this:
- Day 15
- Day 30 (15 + 15)
- Day 45 (30 + 15)
- Day 60 (45 + 15)
- Day 75 (60 + 15)
- Day 90 (75 + 15)
- Day 105 (90 + 15)
- Day 120 (105 + 15)
- And so on...
You can see a pattern here. We're just repeatedly adding 15. It's like counting in fifteens!
The Multiples of 24: Gary's Gaming Schedule
Gary, with his epic gaming, has his sessions every 24 days:
- Day 24
- Day 48 (24 + 24)
- Day 72 (48 + 24)
- Day 96 (72 + 24)
- Day 120 (96 + 24)
- Day 144 (120 + 24)
- And so on...
Again, we're just adding 24 each time. It's Gary's own special countdown!
Finding That Magical Day!
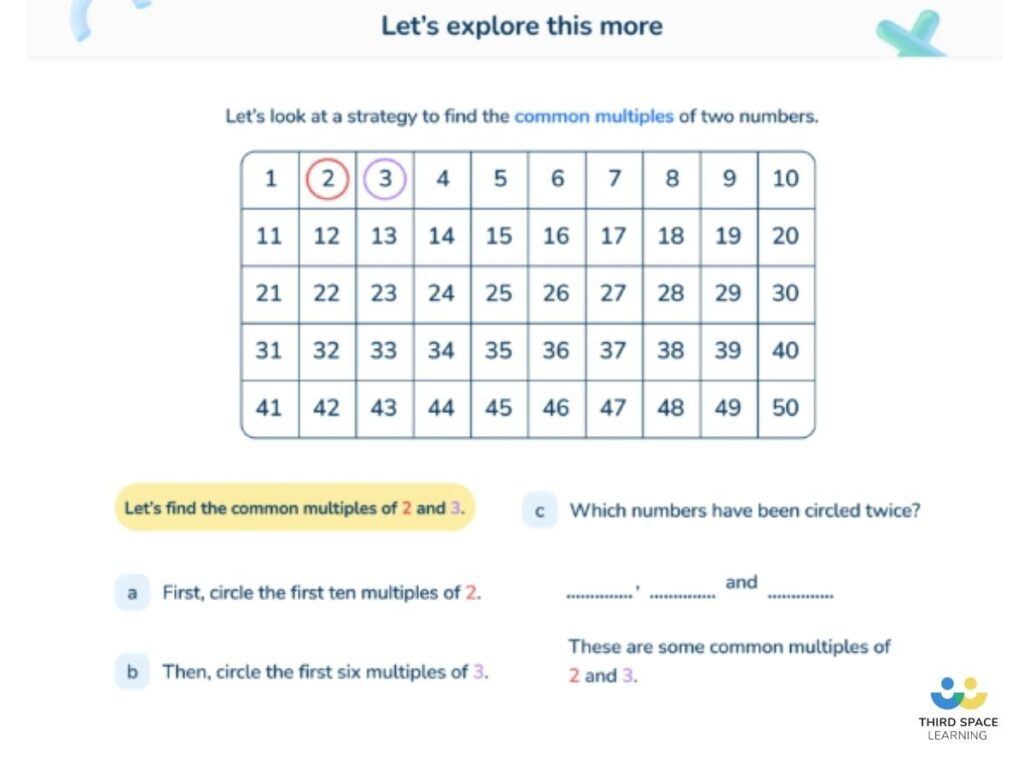
Now for the exciting part! We want to find the smallest day number that appears on both Brenda's and Gary's lists. Let's scroll through our lists and see if we can spot a match.
Brenda's list: 15, 30, 45, 60, 75, 90, 105, 120, ...
Gary's list: 24, 48, 72, 96, 120, 144, ...
Ta-da! Look at that! The number 120 shows up on both lists. And because we're listing them in order, it's the first time they'll sync up. So, on day 120, Brenda will be baking cookies, and Gary will be celebrating a gaming victory. Perfect timing for a surprise!
The Lowest Common Multiple of 15 and 24 is, therefore, 120. It's the smallest number that 15 and 24 can both divide into evenly. 120 divided by 15 is 8, and 120 divided by 24 is 5. Pretty neat, huh?
Why Should You Even Bother? (Besides Cookies and Gaming!)
Okay, so maybe you're not Brenda or Gary. Maybe your life doesn't revolve around baking schedules or epic gaming quests. But understanding LCM isn't just about these fun little stories. It pops up in surprisingly many places!
Think about scheduling in general. If you have two friends who, for some reason, only talk on the phone every 3 days and every 5 days respectively, when's the next time they'll both be on the phone simultaneously? You'd find the LCM of 3 and 5, which is 15. They'll chat together on the 15th day.
It's also super helpful when you're dealing with fractions. If you've ever tried to add fractions like 1/15 and 1/24, you need a common denominator. And what do you think that common denominator should be? You guessed it – the Lowest Common Multiple! Finding the LCM as your common denominator makes the addition (or subtraction) so much simpler. It’s like finding the shortest plank that can be cut into equal pieces of both 15cm and 24cm lengths without any leftover bits.
Imagine you're a chef trying to make a recipe that requires ingredients measured in quantities of 15 grams and 24 grams, and you want to buy in bulk. You'd want to buy a package size that's a multiple of both, and the smallest sensible size would be based on the LCM. This helps avoid waste and makes sure you can get exactly what you need without ending up with a ton of one ingredient and not enough of the other.
Even in more abstract situations, like designing interlocking gears or planning synchronous signals in electronics, the concept of finding a common cycle is crucial. The LCM helps engineers and designers figure out when different cycles will align, preventing conflicts or ensuring smooth operation.
So, while the exact numbers 15 and 24 might not be in your daily vocabulary, the idea behind the Lowest Common Multiple is all about finding harmony, synchronicity, and efficiency. It’s about finding that sweet spot where different rhythms meet.
A Little Trick to Make it Easier
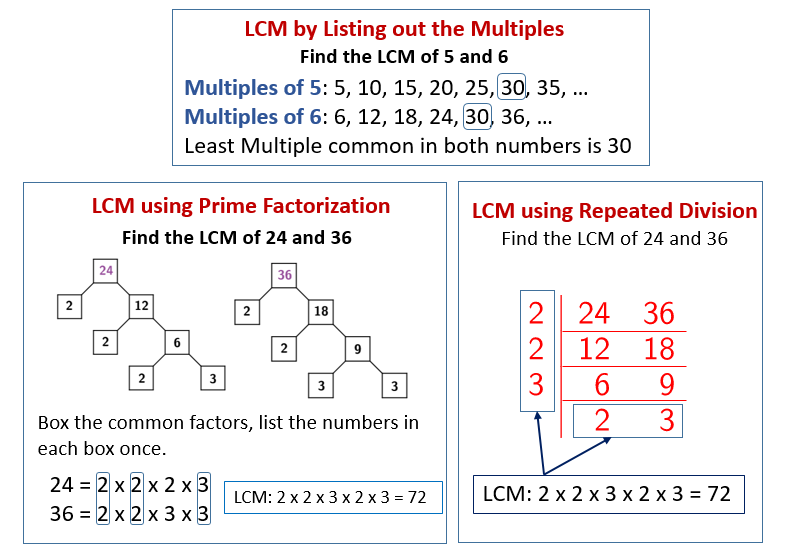
Sometimes, just listing out multiples can take a while, especially with bigger numbers. There's a handy-dandy trick using prime factorization. Don't let the fancy name scare you! Prime numbers are just numbers that can only be divided by 1 and themselves (like 2, 3, 5, 7, 11...).
Let's break down 15 and 24 into their prime factors:
- 15 = 3 x 5
- 24 = 2 x 2 x 2 x 3 (or 2³ x 3)
Now, to find the LCM, you take every prime factor that appears in either number, and you use the highest power of that factor.
- We have a '2' in 24, and the highest power is 2³.
- We have a '3' in both 15 and 24, and the highest power is 3¹ (just 3).
- We have a '5' in 15, and the highest power is 5¹.
So, the LCM is 2³ x 3 x 5 = 8 x 3 x 5 = 24 x 5 = 120. See? Same answer, and often much faster when the numbers get bigger!
It's like collecting all the unique building blocks from both numbers and making sure you have enough of each to build the smallest possible common structure.
In Conclusion (Don't Worry, It's Not a Test!)
So, the next time you hear "Lowest Common Multiple," I hope you don't groan. Think of Brenda and Gary, or the joy of adding fractions smoothly, or just the simple elegance of finding a perfect sync. The LCM of 15 and 24 is 120. It's a small piece of the mathematical puzzle that helps us understand how things align, repeat, and work together. And in a world that can sometimes feel a little chaotic, finding that perfect alignment is always a good thing. Happy syncing!
