How To Solve System Equations By Graphing
Ever feel like you're trying to balance two things at once, and you just know there's a sweet spot where everything works out? Like when you're trying to decide between ordering pizza or tacos for dinner, and you really want both but your wallet is giving you the stink-eye? Or maybe you're planning a road trip and you have a budget for gas and a budget for snacks, and you need to figure out how many delicious, greasy chips you can afford without running on fumes halfway to your destination. Yep, that's kind of what solving system of equations by graphing is all about. It's like finding that magical point where all your competing desires (or, you know, mathematical constraints) meet up for a harmonious high-five.
Think of it like this: you've got two friends, let's call them Alice and Bob. Alice is super into making smoothies, and she always adds a specific amount of spinach and a specific amount of berries. Bob, on the other hand, is all about making his famous chili, and he has his own secret ingredient ratios. Now, imagine they both have a big party coming up and they need to make enough of their creations to feed everyone. They each have a certain amount of ingredients they can use. We're not going to get bogged down in how they make their stuff (that's a whole other adventure!), but what we do want to know is: is there a scenario where they use exactly the same amount of, say, sugar? Or maybe they use the same total amount of ingredients? That's where our graphing detective skills come in.
Let's ditch the food analogies for a sec and get a little more mathy, but still keep it chill. A system of equations is basically just a bunch of equations hanging out together, asking to be solved. When we solve a system, we're looking for the values of the variables (usually 'x' and 'y') that make all the equations in the system true at the same time. It's like finding the one outfit that works perfectly for both your Tuesday work meeting and your casual Friday hangout. Pretty neat, huh?
Now, graphing systems is one of the most visual ways to tackle this. Imagine you have two different roads you could take to get to your favorite ice cream shop. Each road can be described by an equation. When you graph these two equations, you get two lines on a coordinate plane. And guess what? The point where those two lines cross is the spot where you're getting ice cream! It's the ultimate destination that satisfies both routes. Pretty cool, right?
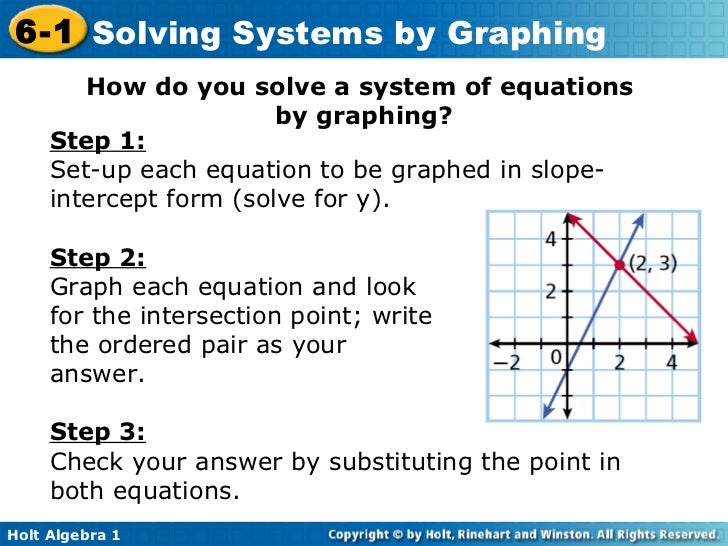
So, how do we actually do this? Grab your favorite colored pens, a trusty ruler, and let's get our graph paper ready. We're going to break it down, step-by-step, like making the perfect sandwich.
Step 1: Get Your Equations Into Graphing Shape
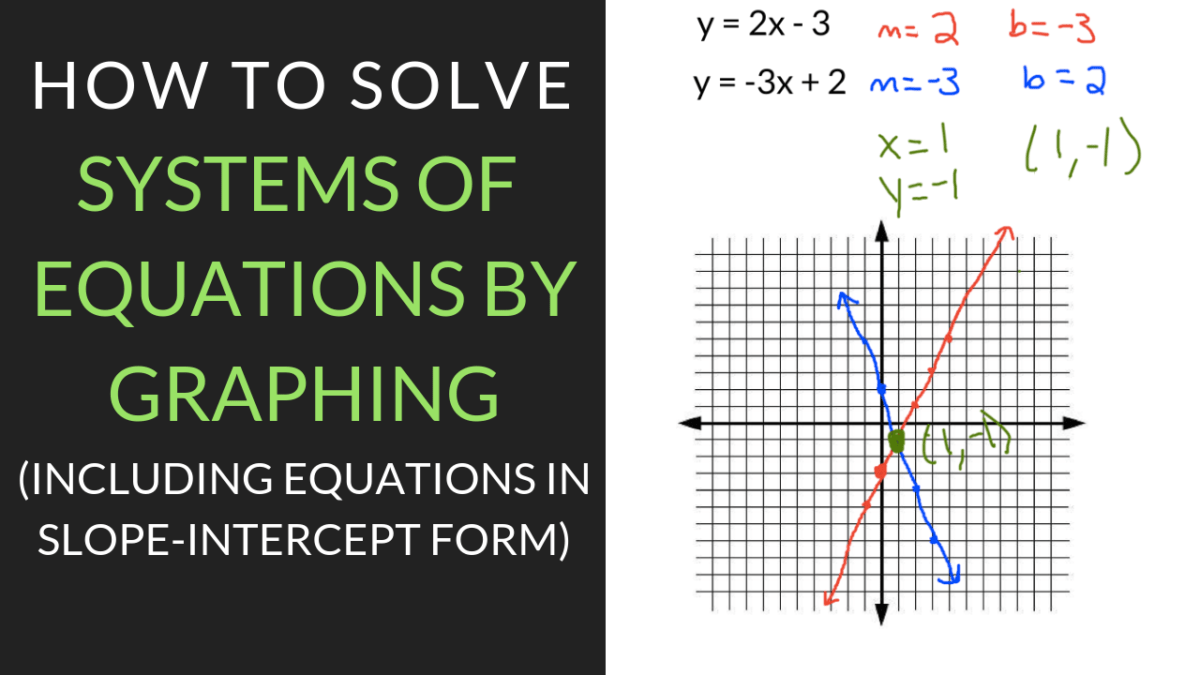
Most of the time, your equations will be in a form that's a bit like a messy closet – everything's in there, but it's not exactly easy to find what you need. The magic shape for graphing is called "slope-intercept form." It looks like this: y = mx + b.
What does that mean? Well, 'y' and 'x' are our usual suspects, the variables. 'm' is the slope, which is basically how steep the line is. Think of it as the incline on a rollercoaster. A big 'm' means a steep climb, a small 'm' means a gentle slope. And 'b' is the y-intercept, which is where the line crosses the y-axis (that's the tall, skinny line on your graph). It's like the starting gate of our rollercoaster.
So, if your equations aren't already in this form (like 3x + y = 5), you need to do a little algebraic rearranging to get the 'y' all by itself on one side. It's like tidying up your closet so you can actually see your clothes. For 3x + y = 5, we'd subtract 3x from both sides to get y = -3x + 5. Now it's in its pretty, graphable shape!
Step 2: Plotting the First Line (It's Not as Scary as it Sounds!)
Once you have your first equation in y = mx + b form, you're ready to put it on the graph. Start with the y-intercept (b). This is your starting point. Go to the y-axis and find that number. Put a dot there. Easy peasy, right?
Now, for the slope (m). Remember that rollercoaster incline? The slope tells you how much the line goes up or down for every step it takes to the right. If your slope is, say, 2, it means for every 1 step to the right, the line goes up 2 steps. If it's -1/2, it means for every 2 steps to the right, the line goes down 1 step. It's like following a secret code to draw your line.
You can think of the slope as a fraction, even if it doesn't look like one. If your slope is 3, you can write it as 3/1. If it's -2, you can write it as -2/1. This helps you count your "rise over run." So, starting from your y-intercept dot, count your "run" (the bottom number of the fraction) to the right, and then count your "rise" (the top number of the fraction) up or down. Make another dot!
Once you have two dots, grab your ruler and draw a straight line connecting them. Make sure to extend it all the way across the graph with arrows on the ends. This line represents all the possible solutions for that first equation. It's like a map of all the routes you could take on your imaginary road trip.
Step 3: Plotting the Second Line (Don't Sweat It!)
Now, you repeat the exact same process for your second equation. If it's not already in y = mx + b form, tidy it up first. Then, find its y-intercept and plot it on the y-axis. Use its slope to find another point, and draw your second line. Again, arrows on the ends!
You're essentially drawing two roads on the same map. It might start to look a little crowded, but don't worry, that's the point!
Step 4: The Grand Finale – Finding the Intersection!
This is where the magic happens! Look at your graph. Do your two lines cross? If they do, that point where they meet is your solution to the system of equations. It's the magical spot where both equations are happy. It's like the universe saying, "Yep, this is it!"
The coordinates of that intersection point (the x and y values) are the answer you're looking for. For example, if the lines cross at the point (2, 3), then x = 2 and y = 3 is the solution to your system. You can then plug these values back into your original equations to double-check – it's like doing a little victory dance to confirm your awesomeness.
What If the Lines Don't Cooperate? (The Not-So-Happy Endings)
Sometimes, life (and math) doesn't always give you that perfect intersection. You might encounter a couple of scenarios that are less than ideal, but still totally solvable:
Scenario A: Parallel Lines (They'll Never Meet!)
Imagine you're on two parallel train tracks. No matter how long you ride, you're never going to bump into the other train. That's what happens when your two lines are parallel. They have the exact same slope (the 'm' value is the same) but different y-intercepts (the 'b' value is different).
In this case, the lines will never intersect. This means there is no solution to your system of equations. It's like trying to find a unicorn and a leprechaun at the same pot of gold – it's not going to happen. Mathematically, this means there are no 'x' and 'y' values that can make both equations true simultaneously.
Scenario B: Identical Lines (They're Practically Best Friends!)
What if your two lines are actually the exact same line? This happens when both the slope (m) and the y-intercept (b) are identical for both equations. It's like having two identical twins who are always in the same place at the same time.
In this situation, the lines overlap completely. Every single point on that line is a solution to both equations. So, instead of one single solution, you have infinitely many solutions. It's like having a never-ending supply of your favorite treat! You can write this as "infinitely many solutions" or use a special symbol if your teacher requires it.
Why Bother With All This Graphing?
You might be thinking, "Okay, this is kind of cool, but can't I just do this with algebra?" And you'd be right! Algebra is super powerful for solving systems. But graphing gives you a visual understanding. It's like seeing a picture of a delicious cake versus just reading the recipe. You get a feel for what's going on.
Plus, in the real world, sometimes things aren't perfectly neat. You might have data that you can model with equations, and graphing is a great way to get an initial feel for the relationship between your variables. It's also a fantastic way to check your algebraic work. If your algebraic solution looks way off from your graph, you know something's up!

So, next time you're faced with a system of equations, don't shy away. Grab your graphing tools and embrace the visual journey. You might just find yourself smiling as those lines intersect, revealing the sweet spot where everything just… works. It's a little bit of math magic, brought to you by the power of pretty lines on a page!
