How To Get Distance From A Velocity Time Graph
Alright, so you've seen these graphs, right? Lines going up, lines going down, maybe a wiggly bit here and there. They look kinda sciency, maybe a little intimidating. But guess what? They're actually your ticket to understanding how far something has gone. Yup, we're talking about distance! And how to snag it from a velocity-time graph. It’s way cooler than it sounds, I promise. Think of it like a treasure map, but for motion.
Imagine you’re telling a story about a race. Your friend asks, "Okay, but how far did they run?" You could just guess, but that’s boring. With a velocity-time graph, you’ve got the exact intel. No more vague estimates!
The Secret Sauce: Area Under the Curve
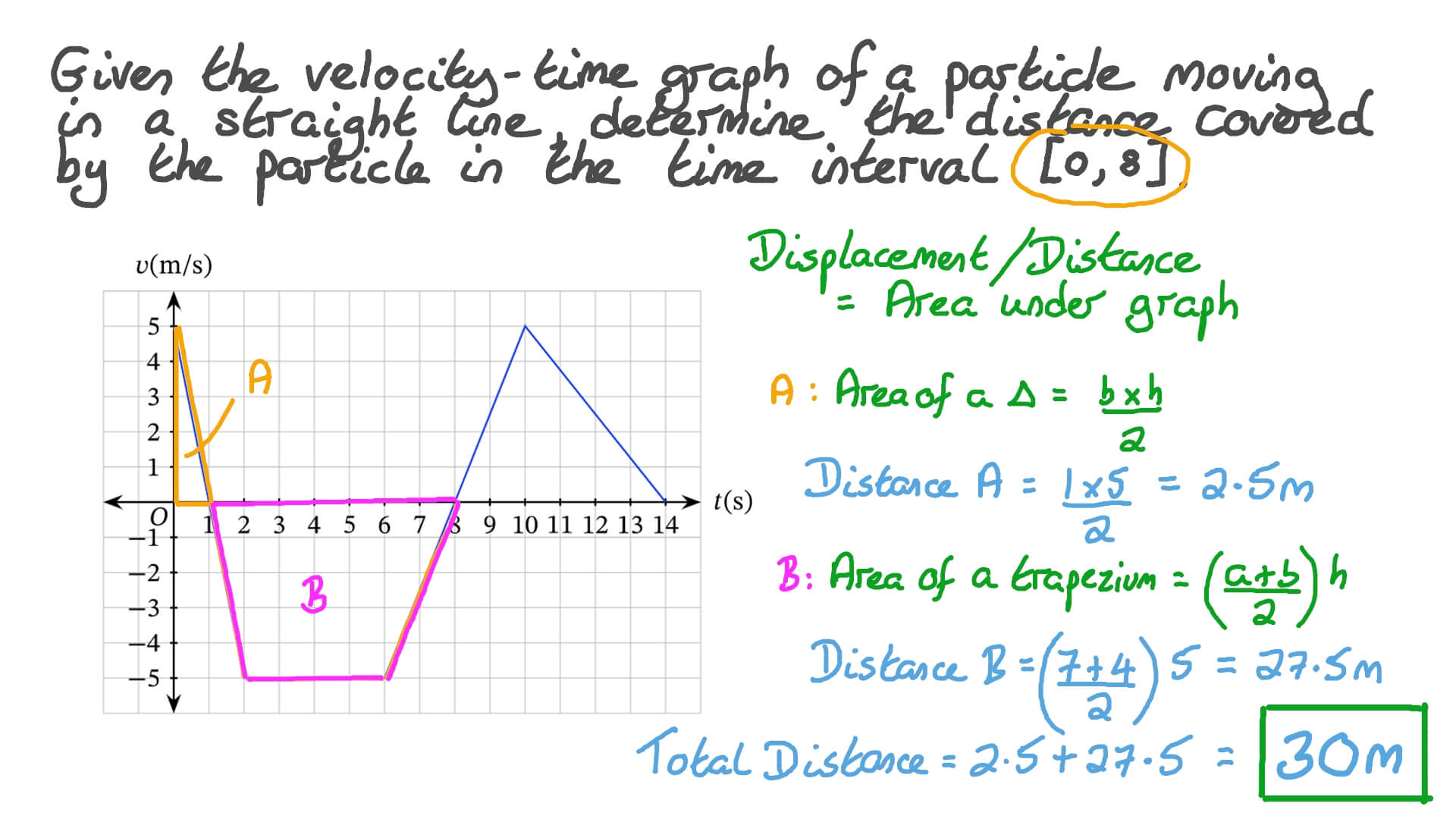
So, here's the big reveal. The absolute, number-one, most important thing to remember is this: the distance traveled is the AREA under the velocity-time graph. Boom. Mic drop. It’s like finding the hidden treasure by coloring in a shape. Seriously, that’s it. The rest is just figuring out how to color.
Think about it. Velocity is speed and direction. Time is, well, time. When you multiply them (which the area calculation basically does), you get distance. It's like magic, but with physics. Pretty neat, huh?
What Kind of Shapes Are We Talking About?
Graphs aren't always neat little squares or triangles, but the principles are the same. Let’s break down the most common scenarios. These are the bread and butter of distance-finding. Get these down, and you’re practically a graphing guru.
Scenario 1: The Straight, Flat Line.
This is the easiest. Imagine a car cruising at a perfectly steady speed. The velocity-time graph is a flat, horizontal line. Let's say it’s at 10 meters per second for 5 seconds. What shape do we have? A rectangle! The width is the time (5 seconds), and the height is the velocity (10 m/s). Area = width x height. So, 5 x 10 = 50 meters. Easy peasy. Your car traveled 50 meters. Congrats, you just calculated distance!
Scenario 2: The Straight, Sloping Line (Upwards!).
Now, imagine that car is speeding up constantly. The line on the graph is going upwards at a steady angle. This is acceleration in action! What shape do we get? A triangle! Or, more accurately, a shape that can be split into a rectangle and a triangle. Let’s say the speed goes from 0 m/s to 20 m/s over 10 seconds. The area under this line is the area of a triangle. The formula for the area of a triangle is ½ x base x height. The base is our time (10 seconds), and the height is our final velocity (20 m/s). So, ½ x 10 x 20 = 100 meters. Your speedy car covered 100 meters.
It's like a little physics puzzle. You see the lines, you identify the shapes, and voila! Distance revealed. Isn't that kinda fun? Like solving a simple math riddle.
Scenario 3: The Straight, Sloping Line (Downwards!).
What if the car is slowing down? This is deceleration, and the line on the graph goes downwards. The math is the same as speeding up, but the context changes. Let’s say it starts at 30 m/s and slows to 10 m/s over 4 seconds. The shape is still a trapezoid (which can be broken into a rectangle and a triangle). The formula for a trapezoid is ½ x (sum of parallel sides) x height. The parallel sides are our velocities (30 m/s and 10 m/s), and the height is our time (4 seconds). So, ½ x (30 + 10) x 4 = ½ x 40 x 4 = 80 meters. The car traveled 80 meters while slowing down. It’s still distance! The graph just shows us the journey.
This is where things get really interesting. Imagine a race car braking. The graph shows the speed dropping. You can see exactly how much ground it covered during that braking period. It’s like watching a slow-motion replay of distance being covered.
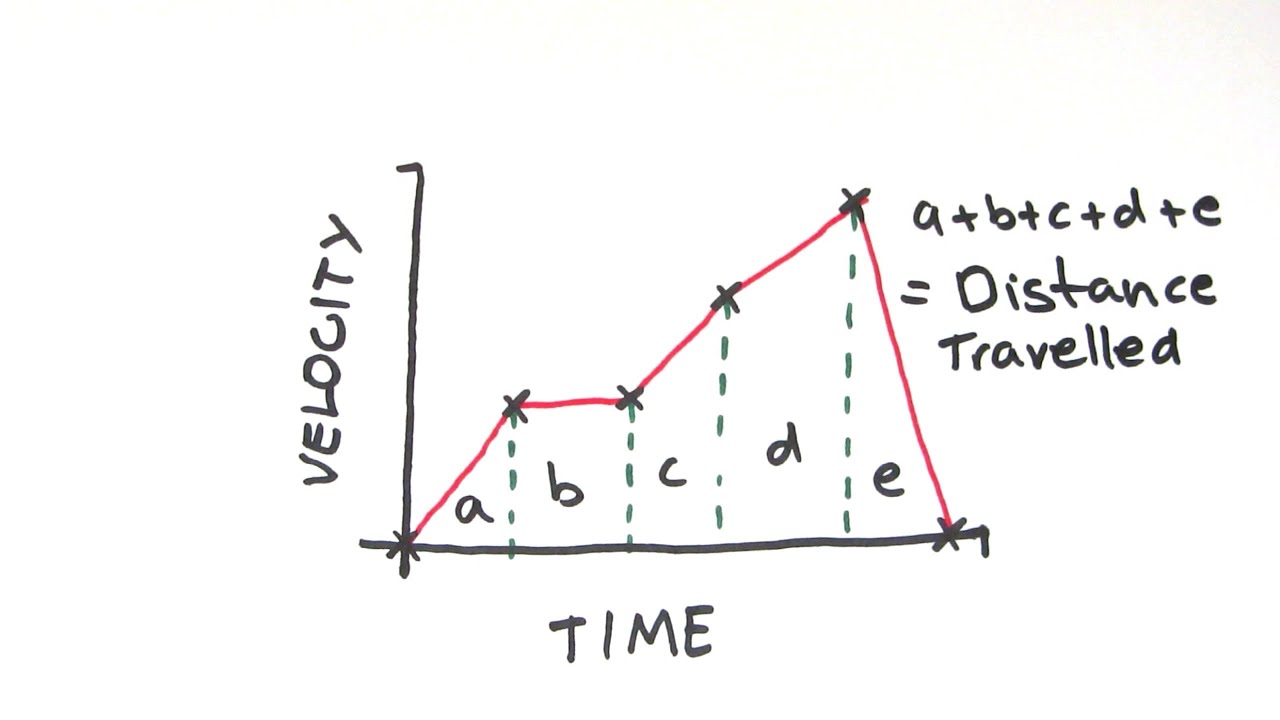
But What About Wiggly Lines?
Ah, the wiggly bits! These are the real adventurers. Real-life motion is rarely perfectly straight. This is where things get a bit more… creative. If you have a curve, you can’t just slap a triangle or rectangle formula on it. That would be like trying to measure a cloud with a ruler. Doesn’t quite work, right?
For these curvy, squiggly lines, we use something called integration. Don’t let the fancy word scare you. In essence, integration is like dividing that wiggly area into an infinite number of tiny, tiny rectangles. You add up the areas of all those infinitesimally small rectangles, and that gives you the total area. It’s a way to precisely measure the area under any shape, no matter how messy.
Think of it like this: Imagine trying to measure the coastline of an island. You can't just use a straight ruler. You have to follow all the little bays and peninsulas. Integration is like having an infinitely detailed ruler that follows every single bump and curve. It’s a super precise way to get your distance measurement.
For us everyday folks, you probably won't be doing complex integrations by hand. Most of the time, you'll be dealing with simpler shapes or using a calculator or software that does the heavy lifting. But it’s good to know the underlying principle! It’s the ultimate method for figuring out distance from any velocity-time graph.
Why is This Fun?
Okay, okay, I know “math is fun” isn’t everyone’s go-to catchphrase. But stick with me! Think about what these graphs represent. They’re snapshots of movement. They can show the exhilarating acceleration of a rocket, the steady cruising of a train, or even the gentle deceleration of a falling leaf (if you’re feeling really whimsical about your physics).
When you look at a velocity-time graph, you’re not just seeing lines. You’re seeing a story unfold. You're seeing how something moved. And by calculating the area, you’re discovering a crucial part of that story: how far it went. It’s like unlocking a secret code of motion.
Plus, there’s a certain satisfaction in taking something that looks complicated and breaking it down into simple geometric shapes. It’s like a visual puzzle! And when you nail that area calculation, you get that little “aha!” moment. It's a tiny victory for your brain.
So next time you see a velocity-time graph, don’t just gloss over it. Give it a second look. See those shapes. Imagine the movement. And remember: the area is your treasure! Go find that distance. Happy graphing!
