How To Find Adjacent Side With Hypotenuse And Opposite
Ever wondered how engineers build bridges that stand tall, or how architects design towering skyscrapers that touch the clouds? Or maybe you’ve just been curious about how those video game characters leap across impossible distances? It all comes down to a bit of mathematical magic, and today, we're going to unravel one of its most dazzling secrets: how to find the adjacent side of a right-angled triangle when you’ve got the hypotenuse and the opposite side in your toolkit. Sounds a bit like a spy mission, doesn't it? But trust us, it's way more fun and surprisingly useful!
This little trick is a cornerstone of trigonometry, and understanding it opens up a world of possibilities. Think of it as having a secret decoder ring for shapes. Why is this so cool? Because right-angled triangles pop up everywhere, from the simplest geometry problems to the most complex scientific calculations. Knowing how to navigate their sides is like having a superpower for problem-solving.
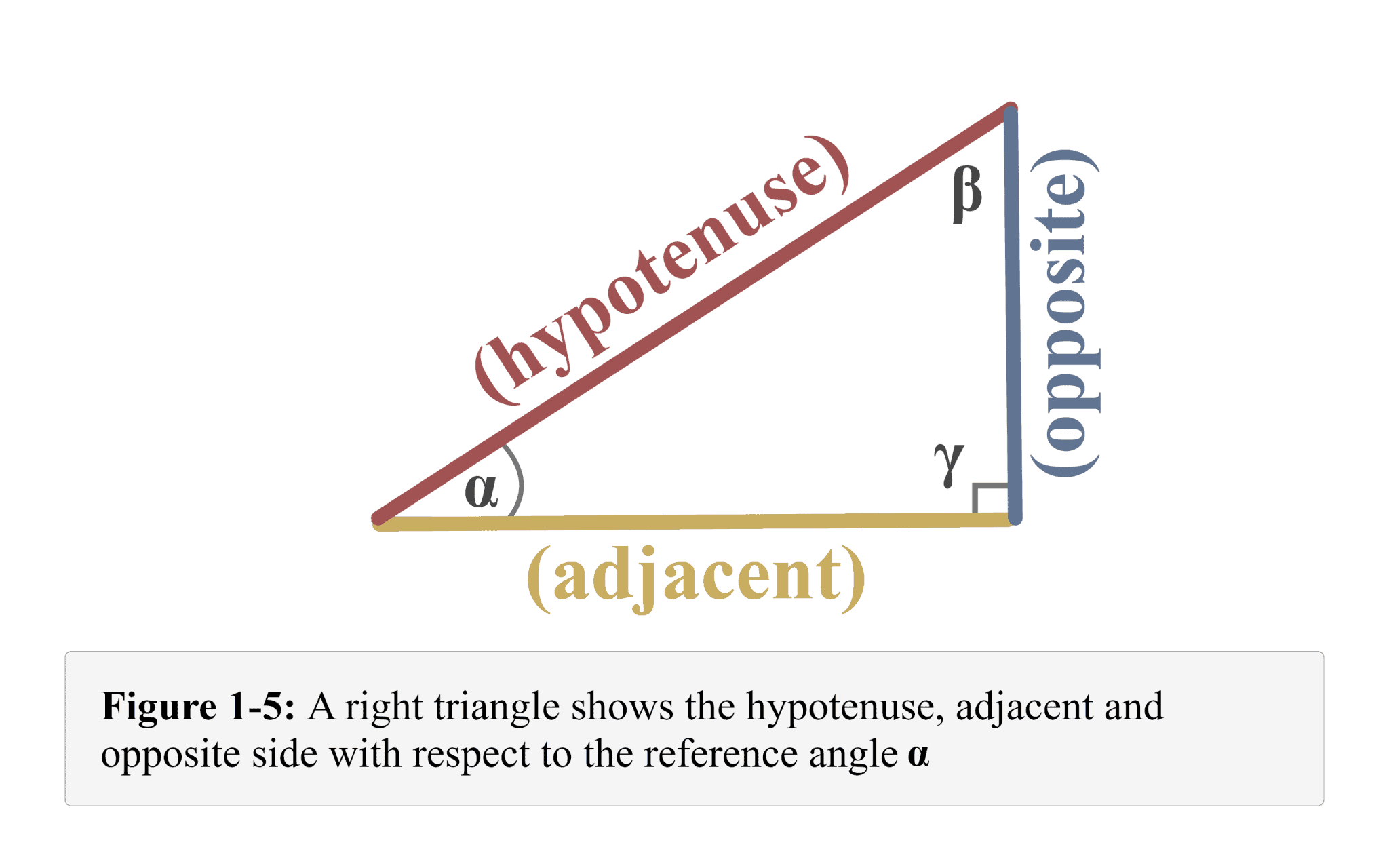
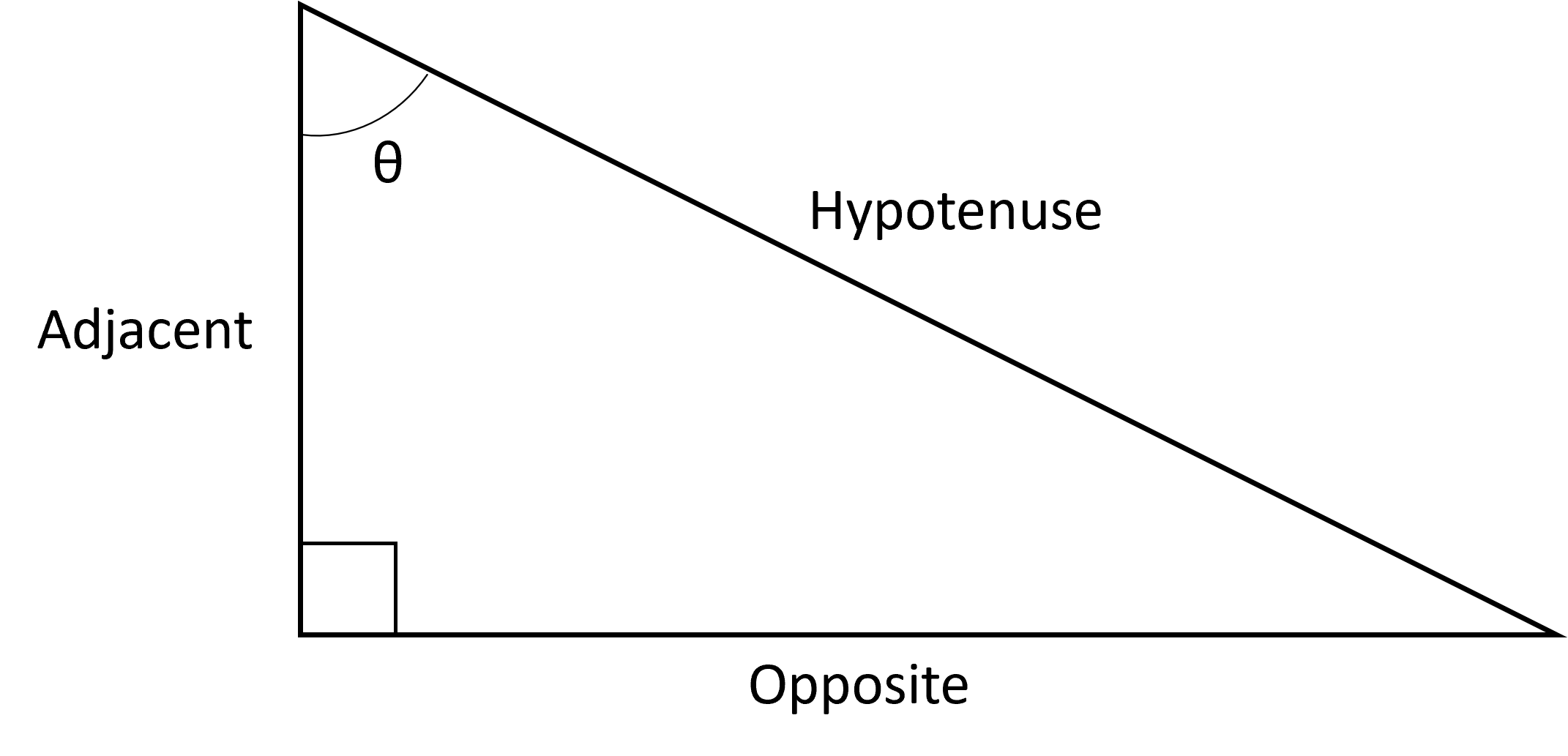
So, what exactly are we trying to achieve here? We're on a mission to discover the length of the adjacent side. Imagine a right-angled triangle. It’s a triangle with one perfect 90-degree corner – like the corner of a square. The longest side, the one that stretches across from the right angle, is our super-important hypotenuse. Then, we have the other two sides: the opposite side (the one directly across from a specific angle we’re focusing on) and the adjacent side (the one next to that same angle, but NOT the hypotenuse). Our goal today is to find the length of that adjacent side.
The benefits of mastering this skill are manifold. For students, it’s a direct path to acing geometry and trigonometry tests. For hobbyists, it means you can tackle DIY projects with more precision, whether it’s figuring out the dimensions for a ramp or planning the layout of a garden. And for anyone interested in the world around them, it’s a way to understand the hidden geometry that shapes our reality. From mapping the stars to designing the circuits in your phone, the principles we’ll explore are fundamental.
The Magic Formula: Unleashing the Power of Cosine!
Now, for the exciting part! How do we actually do this? The key player in our quest is a trigonometric function called the cosine. Don't let the fancy name intimidate you! Think of cosine as a special relationship between an angle and the ratio of two sides in a right-angled triangle. Specifically, the cosine of an angle is equal to the length of the adjacent side divided by the length of the hypotenuse.
This relationship is often summarized by the handy mnemonic SOH CAH TOA. We're focusing on the CAH part: Cosine = Adjacent / Hypotenuse. So, we have our formula:
cos(angle) = adjacent / hypotenuse
But wait, we want to find the adjacent side, not the cosine of the angle itself. That's where a little bit of algebraic rearranging comes in. We can multiply both sides of the equation by the hypotenuse to isolate the adjacent side:
adjacent = hypotenuse * cos(angle)
And there you have it! The formula to find your missing adjacent side. To use this formula, you’ll need two crucial pieces of information:
- The length of the hypotenuse.
- The measure of one of the non-right angles in the triangle. (Remember, we’re looking for the side adjacent to a specific angle.)
Once you have these, you’ll also need a scientific calculator or a trigonometric table to find the cosine of that angle. Most calculators have a dedicated 'cos' button. You'll typically press the 'cos' button, enter the angle's measurement, and it will give you the cosine value.
Let's See It In Action: A Practical Example
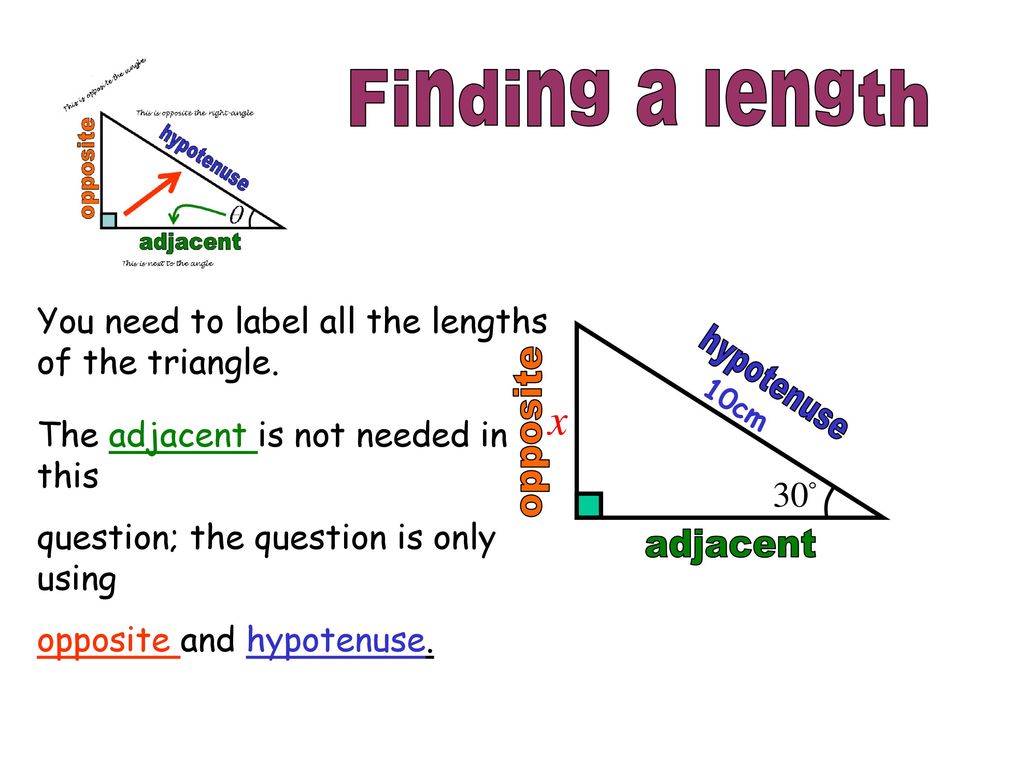
Imagine you're trying to figure out how far away a boat is from the shore. You know the distance from where you’re standing on the cliff to the boat (that’s your hypotenuse – let’s say it’s 100 meters). You also know the angle of depression from your viewpoint to the boat is 30 degrees. The angle of depression is the angle between the horizontal line and the line of sight downwards. For our triangle, this means the angle inside the triangle, at your position on the cliff, is also 30 degrees (due to alternate interior angles with the horizontal line at sea level).
We want to find the horizontal distance from the base of the cliff to the boat. This horizontal distance is our adjacent side to the 30-degree angle.
Using our formula:
adjacent = hypotenuse * cos(angle)
Plugging in our values:
adjacent = 100 meters * cos(30 degrees)
Now, you’d grab your calculator and find the cosine of 30 degrees, which is approximately 0.866.
adjacent = 100 meters * 0.866
adjacent = 86.6 meters
So, the boat is approximately 86.6 meters away from the base of the cliff! Pretty neat, right? You've just used trigonometry to solve a real-world problem!
This skill is not just for math class; it's a fundamental tool for understanding and interacting with the physical world. So, next time you see a right-angled triangle, remember the power of the cosine and how it can help you uncover the secrets of its sides!
