How Many Irrational Numbers Are There Between 1 And 6

Imagine you're standing between the numbers 1 and 6. Not just the whole numbers, mind you. We're talking about all the numbers you can possibly think of in that space. Like 2.5, or 3.14159, or even that weird number pi (π) when it just keeps going and going without repeating. Pretty cool, right? Now, let's get to the juicy part: how many irrational numbers are crammed in there between 1 and 6?

Get ready for a mind-bender, because the answer is… an unbelievable amount. We're not talking about a few. We're not even talking about a million. We're talking about so many, it's practically an infinite party of numbers, all having a blast between our humble little 1 and 6.

Think of it like this: if you were to zoom in on any tiny sliver of space between 1 and 6, say, between 1.1 and 1.2, you'd find a whole universe of numbers. And guess what? A huge chunk of those are the special, mysterious irrational numbers. They're like the wild, unpredictable rock stars of the number world.

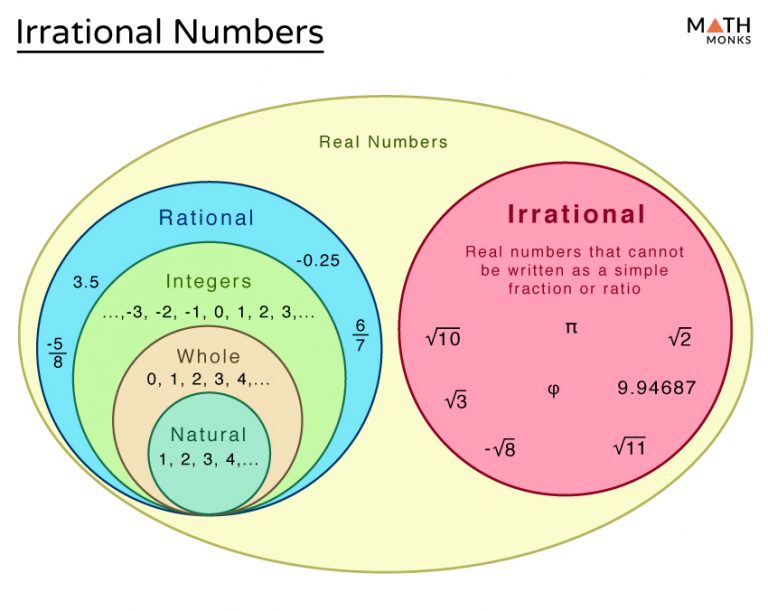
What makes them so special? Well, rational numbers are the well-behaved ones. You can write them as a simple fraction, like 1/2 or 3/4. They're predictable, neat, and tidy. But irrational numbers? They're the rebels. They go on forever and ever without a pattern. They're like a never-ending song that never repeats a chorus. Think of pi (π) again. It's famous for going on forever: 3.1415926535… and it just keeps surprising you with new digits. It’s like a magician pulling endless rabbits out of a hat!

So, between 1 and 6, you have all your normal, predictable numbers like 2, 3, 4, 5. You also have fractions like 1.5, 2.75, 5.9. These are the rational ones. They're the ones you can point to and say, "Yep, I know exactly what that number is."

But then there are the other guys. The ones that make you scratch your head in the most delightful way. Take the square root of 2, for example. It's not a neat little decimal. It's 1.41421356… and it never, ever ends or repeats. That little number is chilling between 1 and 6, having its own private dance party.

Now, imagine you could lay out all the rational numbers between 1 and 6. You could line them up, and you'd have a lot, sure. But then, you'd have all these empty spaces. These empty spaces are begging to be filled. And guess who fills them? The irrational numbers!

It turns out there are infinitely many rational numbers between any two numbers, even if they're super close together. Like between 1.1 and 1.2, you can find 1.11, 1.111, 1.1111, and so on, forever! That alone is mind-boggling.

But the universe of irrational numbers is even bigger. It’s a different kind of infinity, a larger infinity. This is where mathematicians start to get really excited, using fancy terms like "uncountable." But for us, it just means they are an absolutely enormous collection.

So, between 1 and 6, you have numbers like:

• The square root of 2 (which is about 1.414…)
• The square root of 3 (which is about 1.732…)
• The square root of 5 (which is about 2.236…)
• The square root of 10 (which is about 3.162…)
• And so on, for every number between 1 and 6 that isn't a perfect square that can be simplified into a fraction!

These are just a few examples of the irrational crew having a grand old time between 1 and 6.

What makes this so entertaining? It’s the sheer surprise! You think you've got a handle on numbers, and then bam! You realize there's this hidden, infinite world lurking beneath the surface. It’s like discovering secret passages in your own house.

Think about the number line. It looks so simple, just a straight line with numbers marked on it. But it's not just points; it's a swirling, chaotic, beautiful mess of infinitely many numbers, and a huge, wild portion of that mess is made up of the irrational ones. Between 1 and 6, this is particularly true. They’re all packed in there, pushing and shoving, but in a perfectly organized, mathematically sound way.

It’s this idea of endlessness and unpredictability that makes numbers so captivating. The fact that there are more irrational numbers than rational numbers in any given stretch is a bit like finding out there are more stars in the sky than grains of sand on all the beaches in the world. It’s a scale that's hard to truly grasp, but wonderfully fun to ponder.

So, the next time you're looking at the numbers between 1 and 6, remember all those sneaky, never-ending, non-repeating irrational numbers hiding in plain sight. They're having the time of their lives, making the number line a far more interesting and mysterious place than you might have ever imagined. It’s a party you can’t even begin to count!