How Do You Write 0.8 As A Fraction

Ever feel like some numbers are just cooler than others? Like, 0.8? It's got this smooth, sophisticated vibe, doesn't it? It's not a clunky whole number, and it's not a super-short decimal. It’s right there in the middle, doing its own thing. And guess what? This seemingly simple number has a secret life. It’s a secret agent of sorts, capable of transforming into something else entirely! Today, we're going to pull back the curtain on 0.8 and discover its hidden identity. It’s a little bit of mathematical magic, and trust me, it’s way more fun than it sounds. We’re going to explore how to write 0.8 as a fraction, and you’ll see why this process is surprisingly entertaining. Think of it as a puzzle, a fun little brain teaser that reveals a hidden aspect of the numbers we use every day. It’s like finding out your quiet neighbor is actually a world-class chef or an amazing musician. That’s the kind of delightful surprise we're talking about.
So, what exactly is a fraction? Imagine you have a yummy pizza. You cut it into slices. A fraction is just a way to talk about some of those slices, or maybe all of them, or even more than all of them! It’s a part of a whole. Fractions have two parts: a top number (called the numerator) and a bottom number (called the denominator). The denominator tells you how many equal pieces the whole thing is cut into, and the numerator tells you how many of those pieces you’re looking at. It's like saying, "I want 3 slices out of the 8 total slices my pizza was cut into." That's 3/8. See? Pretty straightforward once you get the hang of it. Fractions are everywhere, from recipes ("add 1/2 cup of flour") to measurements ("the shelf is 3/4 inch thick"). They're a fundamental part of how we understand quantities and parts of things.
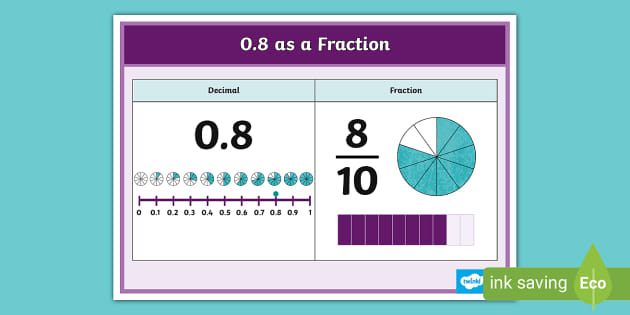
Now, back to our star, 0.8. This decimal number tells us something is less than one whole thing, but quite a bit of it. When you see 0.8, it’s like looking at a pie that’s mostly eaten, but not entirely gone. The "8" in 0.8 is sitting in the tenths place. This is a super important clue! The tenths place means that the whole number has been divided into ten equal parts. So, 0.8 is essentially saying we have 8 of those 10 equal parts. And that, my friends, is the key to unlocking its fractional form. It’s like having a secret handshake that lets you into the world of fractions. This connection between decimals and fractions is one of the most elegant aspects of mathematics, and 0.8 is a perfect, shiny example of it.
"0.8 is essentially saying we have 8 of those 10 equal parts."
So, if 0.8 means 8 out of 10 equal parts, what do you think the fraction looks like? Remember our pizza analogy? The bottom number (denominator) tells us how many equal pieces the whole is divided into. Since 0.8 is in the tenths place, our denominator will be 10. Easy peasy! Now, for the top number (numerator), it tells us how many of those pieces we have. The "8" in 0.8 tells us we have 8 of those tenths. So, the numerator is 8. Put it all together, and the fraction for 0.8 is 8/10! How cool is that? It's like a number is telling you its own recipe. The decimal form gives you a hint, and when you know where to look, you can decode it into its fractional counterpart. This isn't just about memorizing rules; it's about understanding the language of numbers.
But wait, there's more! Fractions, much like people, can sometimes be simplified. That means we can find a simpler, equivalent fraction. Think of it as finding a more streamlined way to say the same thing. For 8/10, we can ask ourselves: "Is there a number that both 8 and 10 can be divided by evenly?" Let’s think about our multiplication tables. Both 8 and 10 are even numbers, meaning they can be divided by 2. So, we can divide both the numerator (8) and the denominator (10) by 2. 8 divided by 2 equals 4. And 10 divided by 2 equals 5. So, 8/10 simplifies to 4/5! This is where the real fun begins. You've taken a number, 0.8, transformed it into a fraction, 8/10, and then discovered an even simpler, more elegant form, 4/5. It’s like finding a hidden gem within a gem. The fraction 4/5 is equivalent to 0.8, meaning they represent the exact same value. It's just a more reduced and often more convenient way to express it.
Why is this so special? Because it shows us that numbers aren't static. They have different ways of being represented, and these different forms can reveal different things about them. The decimal 0.8 is smooth and direct. The fraction 8/10 explicitly shows us it's 8 parts out of 10. And the simplified fraction 4/5 highlights that it's 4 parts out of 5, or two pairs out of two sets of five. It's like looking at the same object from different angles, and each angle reveals something unique and fascinating. This process of converting decimals to fractions, and then simplifying them, is a cornerstone of mathematical literacy. It’s the kind of skill that, once understood, makes you feel a little bit more powerful in the world of numbers. It’s a tangible demonstration of how seemingly different mathematical concepts are actually deeply interconnected. It’s not just about getting the right answer; it’s about appreciating the journey and the elegance of the mathematical structures involved.
So, the next time you see 0.8, don’t just see a decimal. See a number with a hidden talent, a number that can gracefully transform into 8/10 and then even more beautifully into 4/5. It’s a little reminder that there’s often more to things than meets the eye, especially in the fascinating world of mathematics. It's a simple concept, but the implications are profound. It opens the door to understanding more complex fractions and decimals, and how they relate to each other. It's a gateway to a deeper appreciation for the logic and beauty that underpins our quantitative world. So go ahead, impress yourself, impress your friends, and maybe even impress a calculator. You now know the secret: 0.8 is 4/5! And that, my friends, is seriously neat. It’s a small victory in the grand scheme of things, but it’s a victory that empowers you with knowledge and a little bit of mathematical swagger.

The process of writing 0.8 as a fraction is a delightful little exploration. It starts with recognizing the place value of the digit, which immediately tells you the denominator. Then, the digit itself becomes the numerator. Finally, the elegant step of simplification reveals an even cleaner representation. It’s a journey from a decimal form to two different fractional forms, each offering a slightly different perspective. This is why math can be so engaging; it’s not just about calculations, it’s about understanding relationships and transformations. It’s about uncovering the hidden structures that make our world work. So, embrace the simplicity, celebrate the transformations, and enjoy the process of turning a humble decimal into a revealing fraction. It’s a small step, but it’s a step towards a more profound understanding and appreciation of the mathematical universe.
