5 6 7 As An Improper Fraction
So, I was at my niece’s birthday party the other day, a whirlwind of sugar-fueled chaos and questionable dance moves. She’s seven, and her mum, bless her patient soul, was trying to explain fractions. “Okay, sweetie,” she’d said, holding up a pizza cut into eight slices, “if you eat three slices, you’ve eaten three-eighths of the pizza.” My niece, bless her even more chaotic heart, just stared blankly, then proceeded to inhale three more slices. Her mum sighed. I, being the cool aunt, decided to offer my unsolicited, and possibly unhelpful, advice.
“What if,” I’d chimed in, trying to sound worldly and wise, “instead of thinking about what’s left, we think about what’s been eaten? What if she ate, say, ten slices?” The mum just raised an eyebrow. “But there are only eight slices, Auntie! That’s impossible!” And that, my friends, is where we get to the wonderfully weird and often confusing world of improper fractions. And specifically, how numbers like 5, 6, and 7 can totally be improper fractions. Don’t worry, we’re not breaking any mathematical laws here, just bending them a little.
Let's be honest, the term "improper fraction" sounds a bit…judgemental, doesn't it? Like it's been caught shoplifting or something. But in math, it's just a descriptive label, and it’s actually a pretty useful one. Think of it as a fraction where things are a little topsy-turvy compared to what you might expect. We’re talking about fractions where the numerator (that’s the top number) is either equal to or larger than the denominator (the bottom number).

You know, those neat little fractions where the top is smaller than the bottom, like 1/2, 3/4, or 5/8? Those are called proper fractions. They represent a part of a whole, something less than one whole thing. Think of a slice of cake – it’s less than the whole cake, right? Perfectly proper. But what happens when you have more than one whole thing? That’s where the improper fractions strut onto the stage, all confident and slightly oversized.
So, how can a simple number like 5, 6, or 7 become an improper fraction? It's all about context and how we represent a quantity. Let’s take the number 5. As a whole number, it’s just… 5. Five apples, five minutes, five existential crises. But in the world of fractions, 5 can be written as 5/1. See? The numerator (5) is larger than the denominator (1). Boom! Improper fraction.
Why would we even do this? Well, imagine you’re sharing cookies. You have 5 whole cookies, and you want to express that in terms of how many halves you have. Each whole cookie is 2 halves. So, 5 whole cookies is the same as 5 multiplied by 2 halves, which gives you 10 halves. So, 5 whole cookies can be represented as the improper fraction 10/2. Mind. Blown. (Or maybe just slightly bent).
This is the crucial part, the little lightbulb moment you might have when you’re wrestling with these concepts. Any whole number can be written as an improper fraction by simply putting it over the number 1. So, 5 is 5/1, 6 is 6/1, and 7 is 7/1. The numerator (5, 6, or 7) is clearly greater than the denominator (1). Therefore, they are, by definition, improper fractions. It’s almost too easy, isn't it? Makes you wonder what all the fuss is about.
The Pizza Predicament, Revisited
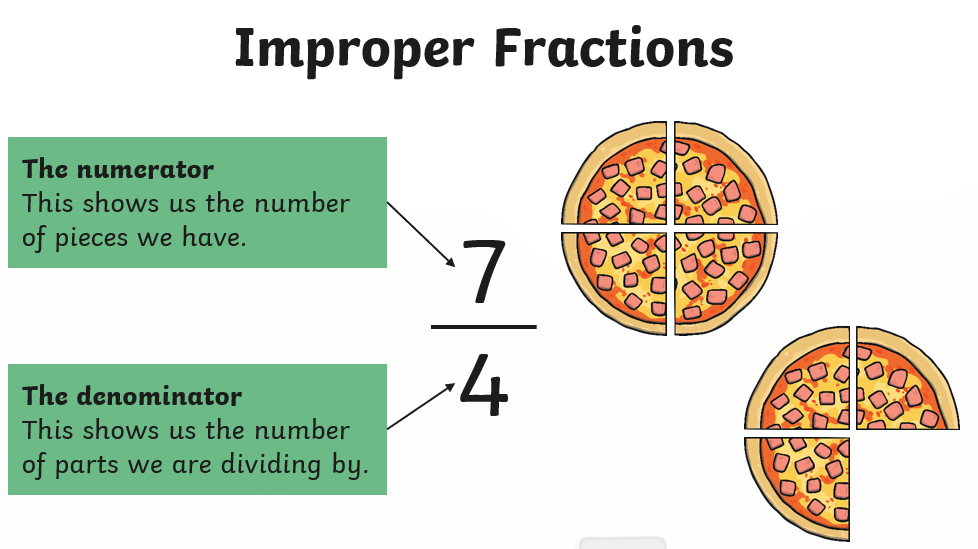
Let’s go back to that pizza party. My niece, in her infinite wisdom, had eaten more than one pizza. If we’d had two pizzas, each cut into 8 slices, and she’d somehow managed to eat 10 slices (which, let’s be honest, is not beyond the realm of possibility for a determined seven-year-old), she’d have eaten 10/8 of a pizza. That’s an improper fraction. The numerator (10) is bigger than the denominator (8). It tells us she ate more than one whole pizza. It’s a handy way to keep track of quantities that go beyond a single unit.
Think about it like this: 10/8 means you have ten slices, and each whole pizza is made up of eight slices. So, you have one full pizza (8/8) and then two more slices left over (2/8). This is where improper fractions start to feel familiar, because 10/8 is just another way of saying 1 and 2/8, or 1 and 1/4. This is called a mixed number – a whole number part and a proper fraction part. Improper fractions are like the slightly messy, but very honest, predecessors to mixed numbers.
So, our number 5, as an improper fraction, 5/1, is equivalent to 5 whole units. If we think of it in terms of halves, it’s 10/2. Or in terms of thirds, it would be 15/3. See? We can have different denominators, but as long as the numerator is equal to or greater than the denominator, it’s an improper fraction. The value remains the same, but the way we express it changes.
And 6? As an improper fraction, it could be 6/1, 12/2, 18/3, 24/4, and so on. Always a numerator that’s at least as big as the denominator. It’s like having 6 whole sandwiches. If you’re sharing them cut into quarters, you’ve got 24 quarters. So, 6 sandwiches is the same as 24/4 of a sandwich. It sounds like a lot, and it is, but it's mathematically sound!
And 7? Well, you guessed it. 7/1, 14/2, 21/3, 28/4… the list goes on. Seven whole pies. If you’re slicing them into sixths for a party, you’ve got 42 slices, making it 42/6 of a pie. More pie than you can shake a stick at, and an improper fraction to boot.
Why Does This Even Matter?
Okay, okay, I can hear you thinking, "This is all well and good, but why should I care about writing 5 as 5/1? What's the big deal?" Great question! It’s all about the flexibility and power that fractions offer in mathematics. When you're working with equations, solving problems, or performing calculations, being able to switch between whole numbers, improper fractions, and mixed numbers is incredibly useful. It’s like having a toolbox with different wrenches – sometimes you need the big one, sometimes the small one. Fractions are that toolbox.
For instance, if you were adding fractions, and you had a whole number, say 3, you’d need to convert it to a fraction with a common denominator. So, 3 would become 3/1 (or 6/2, or 9/3, depending on what you’re adding it to). This conversion is fundamental to performing arithmetic with fractions correctly.
Imagine you’re baking. The recipe calls for 2 and 1/2 cups of flour. That’s a mixed number. But if you're measuring and you have a jug marked in quarter cups, you might need to think of that 2 and 1/2 as 5/2 cups. And if you need to divide that flour equally between two bowls, you’d be dividing 5/2 by 2. This is where understanding improper fractions becomes essential for practical tasks.
It also helps us to intuitively grasp magnitudes. When you see 10/8, your brain immediately says, "Okay, that's more than one whole thing." When you see 3/4, it says, "That's less than a whole thing." This visual and conceptual understanding is built by recognizing both proper and improper fractions.
And let’s not forget the sheer elegance of it. Math, at its best, is about finding efficient and consistent ways to describe the world. Improper fractions are a consistent way to represent quantities that are greater than or equal to one whole unit. They’re not a special case; they’re a fundamental part of the fractional system.
A Little Bit of Irony
There’s a certain irony in the name, though, isn’t there? "Improper." It sounds like something to be ashamed of. But in reality, improper fractions are often the ones doing the heavy lifting. They represent the "more than enough" scenarios, the "extra slices," the "multiple whole items." They’re the fractions that show abundance, not scarcity.
Think about it: a proper fraction is always contained, always neat, always less than one. An improper fraction is expansive, it’s exceeding, it's over the top. It’s the fraction that says, "Yeah, we’ve got more than a whole one here, folks!" And there’s nothing improper about that at all. In fact, it’s often quite glorious.
So, the next time you see a number like 5, 6, or 7, remember that they can easily step out of their whole-number shoes and don the slightly more complex, but incredibly useful, garb of an improper fraction. Just slap a '1' on the bottom and voilà! You’ve got 5/1, 6/1, or 7/1. They’re not breaking any rules; they’re just showing you a different, and often more powerful, way to look at the numbers.
It’s like understanding that a very tall person isn't "improperly tall," they're just… tall. Or a very loud laugh isn't "improperly loud," it's just… loud. The terms are descriptive, not critical. And in the case of fractions, improper ones are essential for describing anything that goes beyond a single, solitary whole.

So, no need to feel intimidated by them. Embrace the "improper." It's where the real action often happens in the world of fractions. And who knows, maybe your niece will eventually get the hang of it, especially if you explain that sometimes, eating more than one whole pizza is actually a perfectly acceptable, and even necessary, mathematical concept. Just don't tell her mum I said that.
